ADT
추상 자료형(Abstract Data Types), 줄여서 ADT는 자료 구조를 사용 방식과 제공하는 동작에 따라 분류하는 방법입니다. ADT는 자료 구조가 메모리에서 어떻게 구현되거나 배치되어야 하는지를 명시하지 않고, 단지 최소한으로 기대되는 인터페이스와 동작의 집합만을 제공합니다. 예를 들어, 스택은 LIFO(Last-In, First-Out; 후입선출) 동작을 갖는 선형 자료 구조를 명시하는 추상 자료형입니다. 스택은 보통 배열이나 연결 리스트를 사용하여 구현되지만, 불필요하게 복잡한 이진 탐색 트리로 구현해도 유효한 구현입니다. 명확히 하자면, 스택이 배열이라거나 그 반대로 말하는 것은 부정확합니다. 배열은 스택으로 사용될 수 있고, 마찬가지로 스택은 배열을 사용하여 구현될 수 있습니다.
추상 자료형은 구현을 명시하지 않으므로, 특정 추상 자료형의 시간 복잡도에 대해 이야기하는 것 또한 부정확합니다. 연관 배열은 평균 검색 시간이 $O(1)$일 수도 있고 아닐 수도 있습니다. 해시 테이블로 구현된 연관 배열은 평균 검색 시간이 $O(1)$입니다.
문제를 더 복잡하게 만드는 것은, 특정 추상 자료형이 거의 항상 특정 자료 구조로 구현되기 때문에 일부 프로그래머들은 두 용어를 혼용해서 사용한다는 점입니다. 예를 들어, 우선순위 큐와 힙, 또는 연관 배열과 해시 테이블이 그렇습니다. 용어가 사용되는 문맥을 통해 보통 구별할 수 있습니다.
Array(Data Structure)
배열(자료 구조)은 순서가 있는 값의 모음을 담을 수 있는 선형 자료 구조의 한 종류입니다. 배열 (ADT)와는 달리, 배열 자료 구조는 값들이 동일한 크기를 가지며 연속된 메모리에 저장되는 구현을 명시합니다. 배열은 매우 보편적이며 프로그래밍에서 가장 오래되고 널리 사용되는 자료 구조 중 하나입니다.
달리 명시되지 않는 한, 이 위키의 나머지 부분에서 "배열"이라는 단어는 추상 자료형이 아닌 자료 구조를 지칭합니다.
배열은 배열(ADT) 및 스택과 같은 추상 자료형을 구현하는 데 자주 사용됩니다. 또한 비효율적인 큐와 양방향 큐를 구현하는 데 사용될 수도 있습니다.
Properties of the Array
가장 간단한 배열 구현은 첫 번째 인덱스의 메모리 주소만 저장합니다. 일부 언어에서는 버퍼 오버플로 오류를 방지하기 위해 배열의 크기도 저장합니다. 주어진 인덱스의 항목을 삽입하고 검색하는 것은 인덱스 $i$를 가져와 항목 크기 $s$(바이트 단위)를 곱한 다음, 기본 메모리 주소 $b$에 더하여 수행됩니다.
0부터 인덱싱하는 언어의 경우, 인덱스의 메모리 주소 $m$은 다음과 같이 주어집니다.
$m=b+si$.
[!example] 다음 C 코드 스니펫을 살펴보겠습니다:
uint32_t prime_numbers[5]; prime_numbers[0] = 2; prime_numbers[1] = 3; prime_numbers[2] = 5; prime_numbers[3] = 7; prime_numbers[4] = 11;1행은 32비트 부호 없는 정수를 담는 길이 5의 배열을 선언합니다. 32비트는 4바이트이므로, 항목 크기 $s$는 4입니다. 이는 우리 배열의 총 크기가 5×4=20 바이트임을 의미합니다. 첫 번째 인덱스에는 임의의 메모리 주소가 할당됩니다; 예를 들어, $b=0xB3A0$라고 가정해 봅시다. 전체 배열은 메모리 주소 $0xB3A0$부터 $0xB3B3$까지 사용합니다.
2-6행은 각각 주어진 인덱스의 메모리 주소를 계산하고 값을 4바이트 부호 없는 정수로 씁니다. 예를 들어, 5행에서 인덱스 3의 메모리 주소는 $0xB3A0+4⋅3=0xB3AC$ 입니다. 따라서 값 7은 주소 0xB3AC에서 시작하는 4바이트 부호 없는 정수로 쓰여집니다.
C에서 크기가 다른 항목들을 배열에 저장하려면, 항목 자체 대신 해당 항목에 대한 포인터를 명시적으로 저장해야 합니다. 이는 자바나 파이썬과 같은 고수준 언어에서 배열이 작동하는 방식입니다. 배열에 원시 항목을 직접 저장하는 대신, 실제 항목에 대한 참조가 저장됩니다. 자바와 파이썬에는 포인터 타입이 없기 때문에 이 모든 것이 암묵적으로 일어납니다. 이로 인한 결과 중 하나는 배열을 순차적으로 순회하는 것이 실제로는 비연속적인 메모리 부분을 접근하는 것일 수 있다는 점입니다. 모든 값이 연속된 메모리 공간에 존재하는 대신, 값들은 메모리의 임의의 위치에 저장되어 서로 멀리 떨어져 있을 수 있습니다. 데이터의 지역성(locality)과 CPU가 이를 효율적으로 캐시하는 능력이 손실됩니다.
배열은 생성될 때 선언되는 고정된 크기를 가집니다. 생성 후 배열 크기를 조절할 수 있게 해주는 더 복잡한 자료 구조는 동적 배열입니다.
Time Complexity
배열은 인덱스 조회 과정이 단순히 정수 곱셈 연산과 정수 덧셈 연산으로 이루어지기 때문에 가장 빠른 자료 구조 중 하나입니다. 이 두 연산은 현대 CPU에서 매우 빠릅니다. 아래는 배열(ADT)에 필요한 기본 함수의 시간 복잡도입니다.
| 연산 | 복잡도 |
|---|---|
| get | $O(1)$ |
| set | $O(1)$ |
Space Complexity
배열은 담고 있는 요소의 수 $n$에 비례하는 선형 공간을 차지합니다. 또한 특정 크기로 초기화되기 때문에 메모리 공간이 낭비되지 않는다는 이점이 있습니다.
공간 - $O(n)$
Two-dimensional Arrays
2차원 배열 또한 연속된 메모리에 저장됩니다. 0부터 인덱싱하는 언어의 경우, 항목 크기가 $s$ 바이트, $r$개의 행, $c$개의 열, 그리고 기본 메모리 주소가 $b$인 배열에서 주어진 인덱스 $i$와 $j$에 있는 항목의 메모리 주소 $m$은 다음과 같이 주어집니다.
$$m=b+s(ci+j)$$.
[!example] 다음 C 코드 스니펫을 살펴보겠습니다:
uint32_t transform[3][2]; transform[0][0] = 37; transform[0][1] = 0; transform[1][0] = 0; transform[1][1] = 39; transform[2][0] = 1; transform[2][1] = 4;1행은 $r=3$개의 행과 $c=2$개의 열을 가진 2차원 배열을 선언하며, 32비트 부호 없는 정수를 담습니다. 32비트는 4바이트이므로, 항목 크기 $s$는 4입니다. 이는 우리 배열의 총 크기가 3×2×4=24 바이트임을 의미합니다. 첫 번째 인덱스에는 임의의 메모리 주소가 할당됩니다; 예를 들어, $b=0xC704$라고 가정해 봅시다. 전체 배열은 메모리 주소 $0xC704$부터 $0xC71B$까지 사용합니다.
2-7행은 각각 주어진 인덱스의 메모리 주소를 계산하고 값을 4바이트 부호 없는 정수로 씁니다. 예를 들어, 7행에서 인덱스 $i=2$, $j=1$의 메모리 주소는 $0xC704+4⋅(2⋅2+1)=0xC718$ 입니다. 따라서 값 4는 주소 0xC718에서 시작하는 4바이트 부호 없는 정수로 쓰여집니다.
이 기술은 n차원 배열을 연속된 메모리에 저장하는 데 일반화될 수 있습니다.
Jagged Arrays
위에서 다룬 2차원 배열은 정의상 항상 직사각형입니다. 종종 이는 당면한 문제에 잘 맞지 않아 공간을 낭비하게 됩니다. 이는 길이가 다른 1차원 배열에 대한 참조를 저장하는 1차원 배열을 사용하여 피할 수 있습니다. 이는 간접 참조 수준을 추가하므로 약간 느리지만, 절약되는 메모리 때문에 종종 그럴 가치가 있습니다. 자바나 파이썬과 같은 고수준 언어는 다차원 배열에 대해 가변 배열만 허용합니다.
Array(ADT)
배열은 정수 인덱스로 접근할 수 있는, 순서가 있는 항목들의 모음을 담는 기본적인 추상 자료형입니다. 이 항목들은 정수와 같은 원시 타입부터 클래스의 인스언스처럼 더 복잡한 타입까지 무엇이든 될 수 있습니다. 배열은 ADT이므로 구현을 명시하지는 않지만, 거의 항상 배열(자료 구조)이나 동적 배열로 구현됩니다.
달리 명시되지 않는 한, 이 위키의 나머지 부분에서 "배열"이라는 단어는 자료 구조가 아닌 추상 자료형을 지칭합니다.
배열은 한 가지 속성을 가집니다: 정수 인덱스를 사용하여 항목을 저장하고 가져온다는 것입니다. 항목은 주어진 인덱스에 저장되며, 나중에 같은 인덱스를 명시하여 가져올 수 있습니다. 이 인덱스가 작동하는 방식은 구현에 따라 다르지만, 보통은 값이 차지하는 배열의 슬롯 번호라고 생각할 수 있습니다. 아래 이미지를 살펴보세요:
 Array
Array
이 배열의 시각적 표현에서, 크기가 6임을 볼 수 있습니다. 6개의 값이 추가되면, 배열의 크기가 조절되거나 무언가 제거될 때까지는 더 이상 값을 추가할 수 없습니다. 또한 배열의 각 "슬롯"에는 연관된 번호가 있음을 볼 수 있습니다. 프로그래머는 이 번호들을 사용하여 배열에 직접 접근해 특정 값을 가져올 수 있습니다. 이 이미지는 1-기반 인덱싱을 사용하고 있음에 유의하세요. 대부분의 언어는 배열의 첫 번째 인덱스가 1이 아닌 0인 0-기반 인덱싱을 사용합니다.
배열을 각각 하나의 항목만 담을 수 있는, 번호가 매겨진 상자들의 그룹으로 생각할 수 있습니다. 상자가 10개 있다고 가정해 봅시다. 이는 우리가 가진 상자의 수보다 많기 때문에 11개의 항목을 저장할 수 없음을 의미합니다. 만약 제 휴대폰을 5번 상자에 보관하고 싶다면, 그곳으로 직접 가서 상자 안에 넣을 수 있습니다. 나중에 5번 상자 안에 무엇이 있는지 보고 싶다면, 다시 그곳으로 직접 가서 안을 들여다보고 제 휴대폰을 볼 수 있습니다.
Minimal Required Functionality
배열은 다양한 구현에 따라 매우 다른 기능을 갖지만, 다음 연산들은 모든 경우에서 찾아볼 수 있습니다. 이 연산들은 더 복잡한 다른 연산들의 기초를 형성합니다.
| 함수 이름* | 제공 기능 |
|---|---|
set(i, v) |
인덱스 _i_의 값을 _v_로 설정합니다. |
get(i) |
인덱스 _i_의 값을 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Two-dimensional Arrays
보드게임이나 FPS 게임과 같은 많은 컴퓨터 게임은 2차원 "보드" 또는 행렬을 사용합니다. 이러한 문제를 다루는 프로그램들은 2차원 공간에 객체를 표현할 방법이 필요합니다. 이를 위한 자연스러운 방법은 2차원 배열을 사용하는 것이며, 여기서 우리는 배열의 셀을 참조하기 위해 i와 j라는 두 개의 인덱스를 사용합니다. 첫 번째 인덱스는 보통 행을, 두 번째 인덱스는 열 번호를 나타냅니다. 이러한 배열을 사용하면 2차원 자료 구조가 필요한 모든 문제를 쉽게 표현할 수 있습니다.
다차원 배열의 개념은 배열의 배열의 배열을 사용할 수 있는 3차원 상황으로도 확장될 수 있습니다. 사실, 이것은 임의의 차원 수로 확장될 수 있습니다.
Lists
리스트는 순차적인 항목을 저장하는 데 사용되는 추상 자료형입니다. 리스트는 Lisp 계열의 프로그래밍 언어와 전반적인 함수형 프로그래밍 언어에서 중요한 개념입니다. 명령형 언어에서는 비슷한 작업을 위해 배열, 큐, 스택을 사용하는 것이 더 일반적입니다.
Characteristics of a List
리스트의 힘은 **헤드(head)**와 **테일(tail)**의 정의에서 나옵니다.
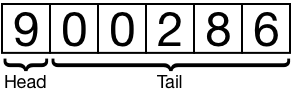
헤드는 리스트의 첫 번째 항목이고, 테일은 나머지 모든 항목입니다. 테일은 그 자체로 리스트이며, 자신만의 헤드와 테일을 가집니다.

이 과정은 모든 테일에 대해 반복될 수 있습니다.
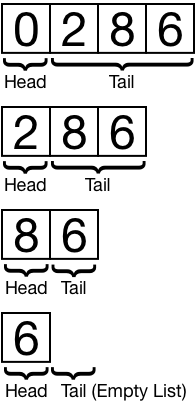
이 속성을 활용하면 최소한의 코드로 재귀를 사용하여 리스트에 대한 연산을 정의할 수 있습니다.
Minimal Required Functionalities
| 함수 이름* | 제공 기능 |
|---|---|
new |
빈 리스트를 생성합니다. |
append |
리스트의 끝에 항목을 추가합니다. |
prepend |
리스트의 시작에 항목을 추가합니다. |
head |
리스트의 시작에 있는 항목을 반환합니다. |
tail |
헤드를 제외한 모든 항목을 반환합니다. 리스트에 항목이 하나만 있으면 빈 리스트를 반환합니다. |
is_empty |
리스트에 항목이 있는지 여부를 나타내는 bool 값을 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Linked List
연결 리스트는 노드(node)라고 불리는 개별 객체에 데이터를 담는 선형 자료 구조입니다. 이 노드들은 데이터와 리스트의 다음 노드에 대한 참조를 모두 가지고 있습니다.
연결 리스트는 효율적인 삽입과 삭제 때문에 자주 사용됩니다. 스택, 큐, 그리고 다른 추상 자료형을 구현하는 데 사용될 수 있습니다.
Properties of Linked Lists
다음 이미지로 연결 리스트를 시각화할 수 있습니다:
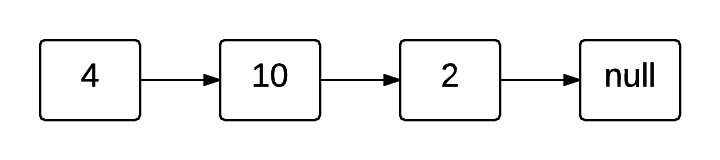 Linked List
Linked List
각 노드는 값(이 경우 정수)과 다음 노드에 대한 참조(포인터라고도 함)를 포함합니다. 마지막 노드(이 경우 2)는 null 노드를 가리킵니다. 이는 리스트가 끝났음을 의미합니다.
연결 리스트는 다른 선형 자료 구조에 비해 몇 가지 중요한 이점을 제공합니다. 배열과 달리, 연결 리스트는 동적 자료 구조이며 런타임에 크기 조절이 가능합니다. 또한, 삽입 및 삭제 연산이 효율적이고 쉽게 구현됩니다.
하지만 연결 리스트에는 몇 가지 단점도 있습니다. 배열과 달리, 연결 리스트는 n번째 항목을 찾는 데 빠르지 않습니다. n 위치의 노드를 찾으려면 연결 리스트의 첫 번째 노드에서 검색을 시작하여 참조 경로를 n번 따라가야 합니다. 또한 연결 리스트는 본질적으로 앞으로 순차적이기 때문에, 뒤로 순회하는 것(끝에서 시작하여 맨 앞으로 모든 노드를 방문하는 것)과 같은 작업은 특히 번거롭습니다.
추가적으로, 연결 리스트는 다음 노드를 참조하는 속성 때문에 배열보다 더 많은 저장 공간을 사용합니다.
마지막으로, 모든 값이 연속된 메모리에 저장되는 배열과 달리, 연결 리스트의 노드들은 임의의, 어쩌면 서로 멀리 떨어진 메모리 위치에 있습니다. 이는 CPU가 연결 리스트의 내용을 배열만큼 효과적으로 캐시할 수 없음을 의미하며, 이는 성능 저하로 이어집니다. 이것이 바로 중간 삽입 및 삭제 기능이 필요하지 않은 고성능 애플리케이션(예: 네트워크 드라이버)에서 큐를 구현하기 위해 연결 리스트 대신 링 버퍼를 사용하는 주된 이유입니다.
Time and Space Complexity
Time
연결 리스트는 리스트 내 노드의 삽입과 삭제에서 가장 큰 이점을 가집니다. 동적 배열과 달리, 리스트의 어느 부분에서든 삽입과 삭제는 상수 시간이 걸립니다.
하지만 동적 배열과 달리, 이 노드들의 데이터에 접근하는 것은 포인터를 통해 전체 리스트를 검색해야 하기 때문에 선형 시간이 걸립니다. 연결 리스트에서는 검색을 최적화할 방법이 없다는 점도 중요합니다. 배열에서는 최소한 배열을 정렬된 상태로 유지할 수 있었지만, 연결 리스트는 길이가 얼마나 될지 모르기 때문에 이진 검색을 수행할 방법이 없습니다.
삽입 - $O(1)$, 삭제 - $O(1)$, 인덱싱 - $O(n)$, 검색 - $O(n)$
Space
연결 리스트는 각 노드마다 두 가지 주요 정보(값과 포인터)를 가집니다. 이는 저장되는 데이터의 양이 리스트의 노드 수에 따라 선형적으로 증가함을 의미합니다. 따라서 연결 리스트의 공간 복잡도는 선형입니다.
공간 - $O(n)$
Doubly Linked Lists
지금까지 우리는 각 셀에서 다음 셀로 한 방향으로만 포인터가 가는 단일 연결 리스트에 대해서만 이야기했습니다. 하지만 양방향으로 포인터가 가는 이중 연결 리스트를 만들 수도 있습니다.
이를 통해 리스트를 양방향으로 순회할 수 있으며, 삭제와 같은 연산을 더 쉽게 만듭니다. 삭제하려는 노드의 앞과 뒤 노드에 대한 포인터가 모두 있기 때문에, 대상 노드 외에 더 이상의 정보가 필요하지 않습니다. 단일 연결 리스트에서는 삭제하려는 노드에 대한 포인터도 필요합니다.
Queues
큐는 스택과 마찬가지로 요소를 추가하거나 제거할 수 있는 위치에 제한이 있는 추상 자료형입니다. 이러한 제한은 요소의 FIFO(First-In, First-Out; 선입선출) 제거를 의무화하며, 줄에 있는 요소의 순서가 유지되어야 합니다.
큐는 구내식당 줄처럼 생각할 수 있습니다: 맨 앞에 있는 사람이 먼저 서비스를 받고, 사람들은 줄의 맨 뒤에 추가됩니다. 따라서 큐에 가장 먼저 들어간 사람이 가장 먼저 서비스를 받고, 가장 최근에 큐에 들어간 사람은 다른 모든 사람 다음에 서비스를 받습니다(FIFO).
큐에서는 요소를 제거하는 **헤드(head)와 요소를 추가하는 테일(tail)에 중점을 둡니다.
Minimal Required Functionalities
큐와 관련된 두 가지 기본 연산이 있습니다.
| 함수 이름* | 제공 기능 |
|---|---|
enqueue(i) |
큐의 테일에 요소 i를 삽입합니다. |
dequeue() |
큐의 헤드에 있는 요소를 제거합니다. |
| 추가적으로, 큐는 계산을 절약하기 위해 다음과 같은 연산과 함께 구현되는 경우가 많습니다. |
| 함수 이름* | 제공 기능 |
|---|---|
size() |
큐의 현재 크기를 반환합니다. |
peek() |
큐를 변경하지 않고 큐의 헤드에 있는 요소를 반환합니다. |
*정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다.
Time Complexity
큐의 시간 복잡도는 사용되는 자료 구조의 종류와 특정 구현에 따라 다릅니다. 아래는 몇 가지 자료 구조와 그들의 인큐 및 디큐에 대한 복잡도 분석입니다.
연결 리스트 큐 인큐 - $O(1)$, 배열 큐 인큐 - $O(1)$, 연결 리스트 큐 디큐 - $O(1)$, 배열 큐 디큐 - $O(n)$
개념은 간단할 수 있지만, 큐를 프로그래밍하는 것은 스택을 프로그래밍하는 것만큼 간단하지 않습니다. 구내식당 줄 예시는 디큐에 있어 연결 리스트가 배열보다 훨씬 빠른 이유를 다시 한번 설명해 줍니다.
[!example] 한 사람이 구내식당 줄을 떠납니다. 이 사람 뒤에 있던 모든 사람은 앞으로 한 걸음씩 움직여야 합니다. 배열에서는 이 과정이 한 번에 한 사람씩, 한 사람만 움직일 수 있습니다. 첫 번째 사람이 떠납니다. 그 다음 두 번째 사람이 첫 번째 사람이 남긴 공간을 채우기 위해 앞으로 나아가고, 그 다음 세 번째 사람이 두 번째 사람이 남긴 공간을 채우기 위해 앞으로 나아가는 식입니다. 줄은 매우 느리게 움직일 것입니다.
최선 그리고 최악의 시나리오에서, 모든 사람이 1만큼 앞으로 움직여야 합니다. 이는 줄에 있는 사람 수에 따라 움직임의 수가 달라지기 때문에 $O(n)$ 시간이 걸립니다.
그러나 연결 리스트의 경우, 단 1명만 움직이면 됩니다. 이것은 전체 줄이 아니라 주문을 받는 사람이 앞으로 나아가는 구내식당 줄과 같습니다. 연결 리스트가 줄의 맨 앞에 있는 사람을 디큐하면, 다음 사람이 줄의 새로운 맨 앞이 됩니다. 그들과 줄에 있는 나머지 사람들은 앞으로 나아갈 필요가 없습니다. 이 연산은 줄의 크기에 의존하지 않기 때문에 $O(1)$, 즉 상수 시간이 걸립니다.
Standard Applications
큐는 항목들이 도착한 순서와 동일한 순서로 검색될 수 있도록 리스트를 구현하는 데 가장 자주 사용됩니다. 운영 체제, 메일 서비스, CPU 스케줄링, 엘리베이터, 키보드 버퍼링 등 다양한 분야에서 많은 실용적인 응용 프로그램을 제공합니다.
큐는 네트워크, 특히 인터넷에서 매우 유용합니다. 예를 들어, 같은 사람에게 두 개의 문자를 보낼 때, 휴대폰에 "2개 중 1개 전송 중"이라고 표시될 수 있습니다. 네트워크는 사용자가 보낸 순서대로 문자가 도착하도록 큐를 사용하여 문자를 저장했습니다. 또는 웹사이트에 데이터를 보낼 때, 데이터가 올바른 순서로 도착하는지 확인하고 싶을 것입니다. 그래서 웹사이트에는 처리 대기 중인 데이터를 수집하는 큐가 있습니다.
Circular Queues
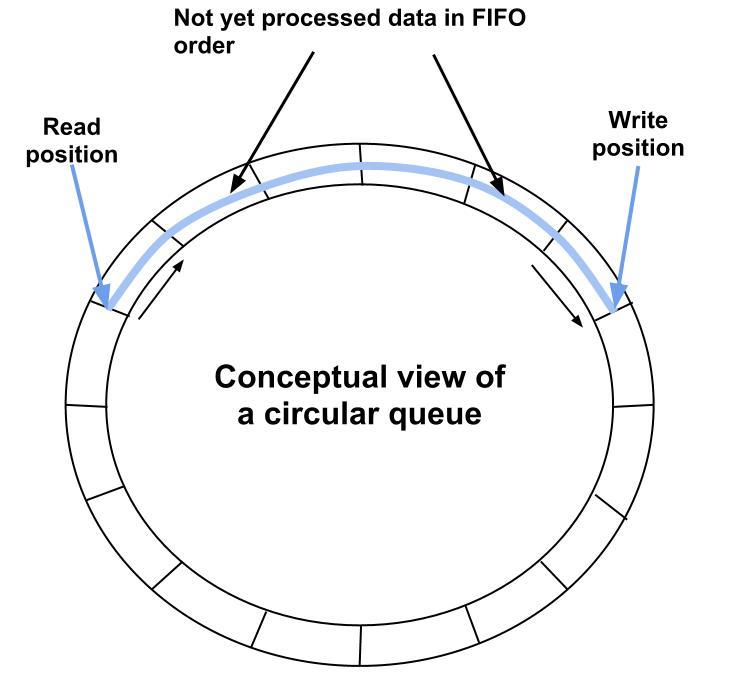 Circular Queue
Circular Queue
큐를 구현하는 몇 가지 기본적인 방법이 있습니다. 첫 번째는 그냥 배열을 만들고 인큐와 디큐를 수용하기 위해 모든 요소를 이동시키는 것입니다. 위에서 보았듯이 이것은 느립니다.
이전 방법의 느린 점은 요소가 많을 때 이동에 시간이 걸린다는 것입니다. 따라서 큐를 구현하는 또 다른 방법은 인큐와 디큐 지점을 이동시키는 것입니다. 앞서 언급한 구내식당 줄 예시에서, 각 사람이 줄을 떠날 때마다 줄이 계속 뒤로 움직인다면, 사람들은 앞으로나 뒤로 움직일 필요가 없어 시간이 절약됩니다.
그러나 이것은 원형 큐에 대한 한 가지 중요한 불변 조건, 즉 최대 용량을 가져야 한다는 것을 도입합니다! 그렇지 않으면 큐의 끝에 도달했는지 알 방법이 없고, 이점은 사라질 것입니다.
이 구현에서는 큐에 자리 표시자(placeholder)가 사용됩니다. 이는 큐가 중간에 비워지더라도 위치를 잃지 않도록 하기 위함입니다. 이것 또한 자료 구조로 리스트를 사용합니다.
이 원형 구현을 이해하려면 배열을 원으로 생각하십시오. 요소가 디큐될 때, 큐는 모든 요소를 큐의 시작 부분으로 이동시키지 않습니다. 대신, 클래스는 큐의 시작을 뒤로 이동시킵니다. 결국, 큐의 시작은 너무 많이 이동하여 큐가 배열의 끝을 넘어 확장될 것입니다. 여기서 원이 등장합니다. 큐가 배열의 끝에 도달하면, 배열의 시작으로 되돌아갑니다. 우리는 큐의 헤드와 테일에 모듈로 연산을 사용하여 이 되돌아가는 작업을 수행합니다.
Double Ended Queues
양방향 큐, 줄여서 덱(deque)은 큐의 일반화된 형태입니다. 헤드 또는 테일에서 요소를 추가하거나 제거할 수 있다는 점을 제외하고는 큐와 정확히 동일합니다.
이 이미지에는 현재 양방향 큐에 3개의 항목이 있습니다 - 양쪽의 추가 공간은 새로운 항목이 들어갈 수 있는 위치를 보여주기 위한 것입니다. 양방향 큐에서는 양쪽에서 항목을 추가하거나 제거할 수 있습니다. 따라서 4를 앞에 추가하면 6의 왼쪽에 4가 나타납니다. 그러면 헤드는 4에 있게 됩니다. 반면에 7을 뒤에 추가하면 2의 오른쪽에 7이 나타납니다. 그러면 테일은 7에 있게 됩니다.
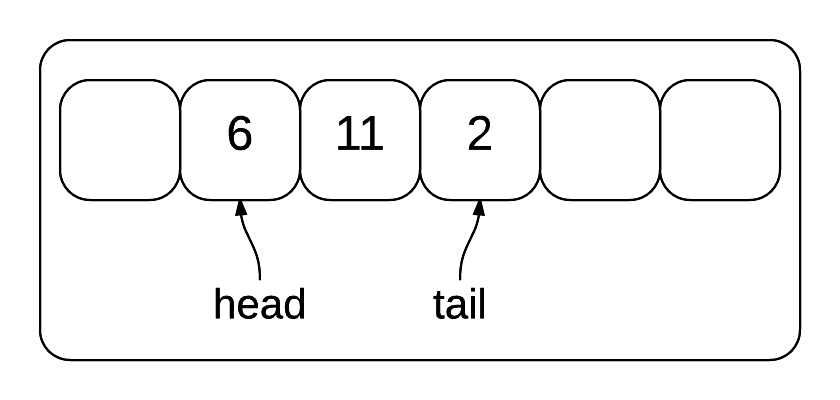 A deque with both a head and a tail
A deque with both a head and a tail
양방향 큐는 식당에서 기다리는 사람들의 줄로 생각할 수 있습니다. 큐에서처럼 사람들은 줄의 앞에서 도움을 받을 수 있고, 줄의 뒤에 합류합니다. 그러나 큐와 달리 두 가지 더 일어날 수 있습니다. 이 줄에서는 줄의 끝에 있는 사람들이 조급해지면 일찍 떠날 수 있고, 이미 주문한 후에 조미료를 요청하러 돌아올 수도 있습니다. 따라서 사람을 추가하고 제거하는 것이 줄의 양쪽 끝에서 일어날 수 있습니다.
Minimal Required Functionalities
양방향 큐에는 여섯 가지 기본 연산이 있습니다.
| 함수 이름* | 제공 기능 |
|---|---|
append(i) |
큐의 테일에 요소 i를 추가합니다. |
prepend(i) |
큐의 헤드에 요소 i를 추가합니다. |
delete_last() |
큐의 테일에 있는 요소를 제거합니다. |
delete_first() |
큐의 헤드에 있는 요소를 제거합니다. |
examine_last() |
큐의 테일에 있는 요소를 반환합니다. |
examine_first() |
큐의 헤드에 있는 요소를 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
일반적으로 이러한 연산은 연결 리스트와 같은 자료 구조로 구현됩니다. 연결 리스트는 선형 추상 자료형을 매우 쉽게 업데이트할 수 있게 해줍니다. 사용되는 자료 구조에 관계없이, 각 연산을 수행할 수 있도록 덱의 헤드와 테일에 대한 참조를 계속 유지하는 것이 필수적입니다.
Time Complexity
덱의 시간 복잡도는 사용되는 자료 구조의 종류와 특정 구현에 따라 다릅니다. 아래는 이중 연결 리스트와 동적 배열에 대한 복잡도 분석입니다.
| 연산 | 이중 연결 리스트 | 동적 배열 |
|---|---|---|
| append | $O(1)$ | $O(1)$ |
| prepend | $O(1)$ | $O(n)$ |
| delete_last | $O(1)$ | $O(1)$ |
| delete_first | $O(1)$ | $O(n)$ |
| examine_last | $O(1)$ | $O(1)$ |
| examine_first | $O(1)$ | $O(1)$ |
배열의 경우, 여전히 줄처럼 생각할 수 있습니다. 줄의 첫 번째 사람을 제거하면 모든 사람을 앞으로 이동시켜야 하므로 런타임은 $O(n)$입니다. 그러나 줄의 마지막 사람을 제거하면 - 아마도 그냥 줄을 떠나는 경우 - 다른 사람을 이동시킬 필요가 없습니다. 따라서 그 런타임은 $O(1)$입니다. 사람을 그 줄에 추가하는 경우도 같은 논리가 적용됩니다.
연결 리스트 구현에서는 모든 것이 상수 시간입니다. 왜냐하면 어떤 연산이든 해당 요소와 그 이웃에 대한 포인터를 수정하기만 하면 되기 때문입니다. 연결 리스트 구현은 종종 덱의 테일에 대한 포인터를 가지고 있습니다. 이것은 연결 리스트 구현을 매우 빠르게 만듭니다.
Applications
덱은 스택 그리고 큐의 원리를 모두 보여주기 때문에 많은 다른 시나리오에서 유용합니다. 한 예는 분산 컴퓨팅 및 스케줄링입니다. 여러 컴퓨터가 다양한 작업을 완료하려고 할 때, 각 컴퓨터는 먼저 자신의 목록에 있는 첫 번째 작업을 가져오는 것으로 시작합니다. 해당 작업이 완료되면 폐기되지만, 중단되면 목록의 맨 앞으로 다시 푸시됩니다. 그런 다음, 단일 컴퓨터가 자신의 목록을 완료하면 다른 컴퓨터 목록의 마지막 요소를 가져갈 수 있습니다.
큐의 또 다른 중요한 응용 분야는 네트워킹입니다. 큐와 마찬가지로 네트워크 데이터는 선입선출 방식으로 덱에서 처리됩니다. 그러나 특정 데이터 패킷이 너무 오래 기다렸다면, 떠나서 다른 곳을 시도하기로 선택할 수 있습니다. 이런 식으로 양쪽 끝에서 제거하는 덱의 기능은 매우 유용합니다.
Stacks
스택은 요소를 추가하고 제거할 수 있는 위치에 제한을 두는 추상 자료형입니다. 좋은 비유는 스택을 책 더미로 생각하는 것입니다; 맨 위의 책만 제거할 수 있고, 맨 위에만 새 책을 추가할 수 있습니다. 다른 추상 자료형과 마찬가지로, 스택은 연결 리스트나 배열과 같은 다양한 자료 구조로 구현될 수 있습니다. 스택은 요소의 순서를 뒤집거나, 폴리시 표기법(polish strings)을 평가하는 등 다양한 응용 분야를 가집니다.
Characteristics of a Stack
스택의 구별되는 특징은 항목의 추가 또는 제거가 같은 끝에서 일어난다는 것입니다. 이 끝은 일반적으로 "탑(top)"이라고 불립니다. 그 반대쪽 끝은 "바닥(bottom)"으로 알려져 있습니다. 스택이 정렬되는 원리는 LIFO(Last-In First-Out의 약어)라고 불립니다. 책 더미에서, 우리가 더미에 추가한 마지막 책이 책을 제거할 때 반드시 나와야 하는 책입니다.
때로는 스택이 최대 용량을 갖도록 구현되기도 합니다. 이 경우, 스택에 할당된 공간이 완전히 사용되면 더 이상 요소를 푸시할 수 없으며, 그렇게 하려는 시도는 스택 오버플로 오류를 발생시킵니다. 이는 프로그래밍 세계에서 가장 흔하게 접하는 오류 중 하나로, Q&A 웹사이트 stackoverflow.com의 이름에 영감을 주었습니다. 그 반대도 일어날 수 있는데, 스택이 비어 있을 때 팝을 시도하는 경우입니다: 이는 스택 언더플로 오류를 발생시킵니다.
Minimal Required Functionalities
스택과 관련된 두 가지 기본 연산이 있습니다.
| 함수 이름* | 제공 기능 |
|---|---|
push(i) |
스택의 맨 위에 요소 i를 삽입합니다. |
pop() |
스택의 맨 위에 있는 요소를 제거합니다. |
스택은 종종 다음과 같은 함수와 함께 구현됩니다.
| 함수 이름* | 제공 기능 |
|---|---|
size() |
스택의 현재 크기를 반환합니다. |
peek() |
스택을 변경하지 않고 스택의 맨 위에 있는 요소를 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Time Complexity
스택의 시간 복잡도는 사용하고 있는 자료 구조의 종류와 구축하는 특정 구현에 따라 다릅니다. 아래는 연결 리스트와 배열이 복잡도 면에서 크게 다르지 않다는 것을 설명합니다.
| 연결 리스트 | 배열 | |
|---|---|---|
| Push | $O(1)$ | $O(1)$ |
| Pop | $O(1)$ | $O(1)$ |
스택은 큐와 달리, 리스트의 한쪽 끝에서만 연산을 수행합니다. 이 불변 조건은 과정을 훨씬 쉽게 만듭니다. 우리 책 더미에서, 맨 위가 어디인지 이미 알고 있었기 때문에 책을 추가하는 것은 매우 쉬웠습니다. 마찬가지로, 맨 위 책을 제거하는 것도 어디에 있는지 알기 때문에 똑같이 쉽습니다. 모든 연산이 한 지점에서 일어나기 때문에 나머지 더미를 훑어볼 필요가 없습니다.
Associative Arrays
맵(map) 또는 딕셔너리(dictionary)라고도 불리는 연관 배열은 데이터를 (키, 값) 쌍으로 저장할 수 있는 추상 자료형입니다.
연관 배열을 전화번호부 목록처럼 생각할 수 있습니다. 이 목록에서, 당신은 사람의 전화번호를 찾아 그 사람의 이름을 조회할 수 있습니다. 이름은 값이고 번호는 키입니다. 이 목록은 다음 표와 같을 것입니다.
| 전화번호 | 이름 |
|---|---|
| 1-203-456-4657 | John Doe |
| 1-964-725-5617 | Jane Smith |
| 1-275-486-8562 | Daniel Brown |
| 1-347-374-3412 | John Doe |
연관 배열에는 두 가지 중요한 속성이 있습니다. 모든 키는 한 번만 나타날 수 있으며, 마치 모든 전화번호가 전화번호부에 한 번만 나타날 수 있는 것과 같습니다. 그리고 모든 키는 하나의 값만 가질 수 있으며, 마치 모든 전화번호가 한 사람만 가리킬 수 있는 것과 같습니다. 이 목록에 두 사람이 같은 이름을 가질 수는 있으므로, 특정 값이 연관 배열에 두 번 이상 나타날 수 있다는 것을 기억하는 것이 중요합니다.
Minimal Required Functionalities
연관 배열에는 네 가지 기본 연산이 있습니다.
| 함수 이름* | 제공 기능 |
|---|---|
insert(key, value) |
연관 배열에 (키, 값) 쌍을 추가합니다. |
remove(key) |
연관 배열에서 키의 쌍을 제거합니다. |
update(key, value) |
기존 키에 값을 할당/업데이트합니다. |
lookup(key) |
이 키에 할당된 값을 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Time Complexity
연관 배열의 특정 구현은 실행 시간에 큰 영향을 미칩니다.
| 연산 | 배열 | 레드-블랙 트리 | 해시 테이블 |
|---|---|---|---|
| insert | $O(n)$ | $O(\log(n))$ | $O(1)$** |
| remove | $O(n)$ | $O(\log(n))$ | $O(1)$** |
| update | $O(n)$ | $O(\log(n))$ | $O(1)$** |
| lookup | $O(n)$ | $O(\log(n))$ | $O(1)$** |
**충돌 처리 방식에 따라 다름.
위와 같이 배열을 사용하는 구현은 매우 비효율적입니다. 어떤 연산을 하든, 최악의 경우 배열의 모든 쌍을 순회해야 합니다. 그런 이유로 연관 배열은 배열을 사용하여 거의 구현되지 않습니다.
레드-블랙 트리는 배열보다 훨씬 빠릅니다. 이진 탐색 트리이기 때문에 $O(\log n)$ 시간 안에 검색할 수 있습니다. 이것은 배열과 비교할 때 모든 연산을 더 빠르게 만듭니다.
해시 테이블은 연관 배열이 컴퓨터 과학에서 매우 인기 있는 이유입니다. 해시 함수를 도입함으로써, 구현자는 같은 키가 매번 같은 값으로 해시될 것을 보장할 수 있습니다. 그러면 조회가 빠릅니다. 올바른 셀을 보기만 하면 값을 찾을 수 있기 때문입니다. 서로 다른 키가 같은 값으로 해시될 때 충돌이 발생할 수 있다는 점에 유의하는 것이 중요합니다. 이러한 충돌을 해결하는 여러 방법이 있으며(모두 실행 시간에 다양한 영향을 미침), 일반적으로 충돌은 바람직하지 않습니다.
Applications of Associative Arrays
연관 배열은 광범위한 컴퓨터 과학 분야에서 사용됩니다. 메모이제이션(memoization)과 같은 프로그래밍 패턴 및 패러다임에서 자주 사용됩니다. 이 기술은 정보의 저장과 빠른 검색을 강조하며, 메모는 종종 해시 테이블을 사용하여 구현됩니다.
자바스크립트의 모든 객체는 실제로는 연관 배열입니다. 인기 있는 웹 통신 표준인 JSON 또한 연관 배열입니다. JSON은 node.js와 같은 자바스크립트 기반 웹 플랫폼의 부상과 함께 최근 인기를 얻었습니다.
NoSQL 데이터베이스라고 불리는 전체 데이터베이스 유형은 연관 배열을 기반으로 합니다. 이러한 데이터베이스는 (키, 값) 쌍을 저장하기 위해 연관 배열을 사용합니다. 이 유형의 데이터베이스는 빠른 데이터 검색에 특화되어 있습니다. 해시 테이블과 정확히 같습니다.
Hash Tables
해시 테이블은 연관 배열을 구현하는 데 가장 일반적으로 사용되는 자료 구조입니다. 평균 검색 시간이 $O(1)$인 것이 특징이며, 캐싱, 인덱싱 및 기타 시간이 중요한 작업에 사용하기에 효율적인 자료 구조입니다.
Minimal Implementation
해시 테이블은 고정된 크기의 배열을 사용하여 구현됩니다. 키/값 쌍을 삽입하기 위해, 먼저 키가 해시됩니다. 해시는 그냥 큰 정수이므로, 해시를 배열의 크기로 나눈 나머지를 취하여 인덱스를 얻습니다. 그런 다음 키/값 쌍은 해당 인덱스의 버킷에 삽입됩니다.
버킷은 생일 문제(birthday problem)가 해시 충돌이 불가피하다고 말하기 때문에 필요합니다. 그래서 각 인덱스가 단일 키/값 쌍을 저장하는 대신, 쌍들의 버킷을 저장합니다. 가장 기본적인 구현에서, 버킷은 연결 리스트를 사용하여 구현됩니다.
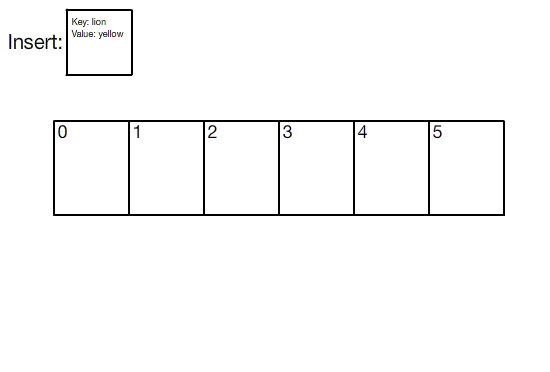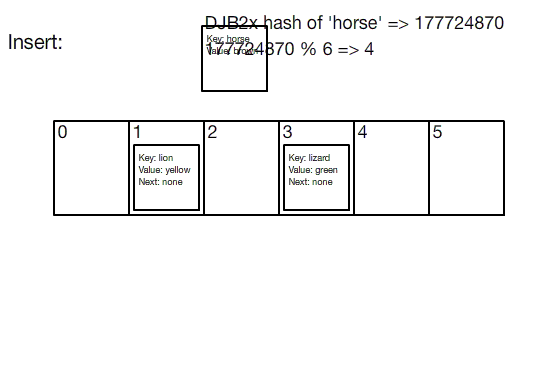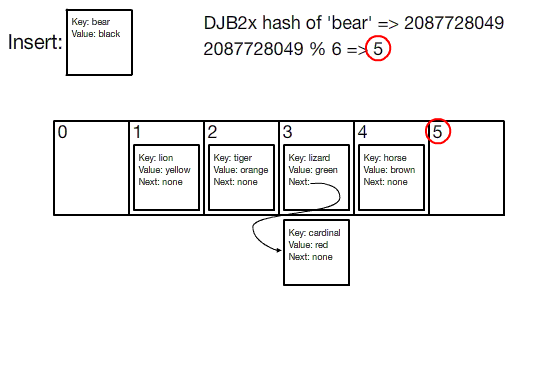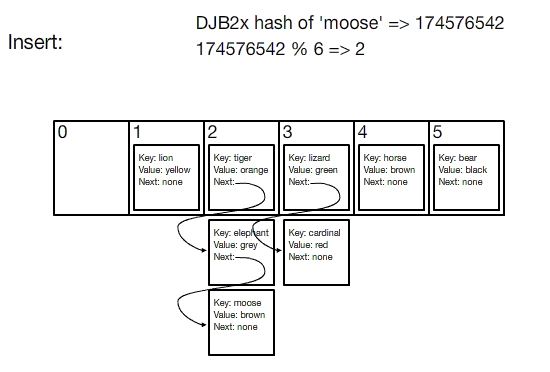 Visualization of hash table insertion
Visualization of hash table insertion
버킷 배열의 크기가 해시 테이블에 저장될 수 있는 키/값 쌍의 수를 제한하지 않는다는 점에 유의하십시오. 위 애니메이션에서, 버킷 배열의 길이는 6이지만 8개의 키/값 쌍이 삽입됩니다. 버킷 수에 대한 쌍의 수의 이 비율을 **로드 팩터(load factor)**라고 합니다.
$_{\text{로드 팩터=쌍의 수/버킷의 수}}$
로드 팩터가 증가함에 따라 충돌이 발생할 가능성이 높아집니다. 충돌이 점점 더 많이 발생하면 성능이 저하됩니다. 절대적으로 최악의 경우, 버킷이 하나뿐인 해시 테이블은 검색, 삽입, 삭제 시간이 $O(n)$인 연결 리스트처럼 동작합니다.
 Bucket length as a function of load factor
Bucket length as a function of load factor
Asymptotic Complexity
| Average | Worst | |
|---|---|---|
| Space | O(n) | O(n) |
| Search | O(1) | O(n) |
| Insert | O(1) | O(n) |
| Delete | O(1) | O(n) |
Sets(ADT)
집합은 반복되지 않는 값의 리스트를 저장할 수 있게 해주는 추상 자료형의 한 종류입니다. 그 이름은 유한 집합의 수학적 개념에서 유래했습니다.
배열과 달리, 집합은 순서가 없고 인덱싱되지 않습니다. 집합을 당신이 아는 사람들로 가득 찬 방으로 생각할 수 있습니다. 그들은 방 안을 돌아다니며 순서를 바꿀 수 있지만, 그 방에 있는 사람들의 집합을 변경하지는 않습니다. 게다가, 복제된 사람은 없습니다(자신을 복제한 사람을 알지 않는 한). 이것이 집합의 두 가지 속성입니다: 데이터는 순서가 없고 중복되지 않습니다.
집합은 수학적 집합론에서 가장 큰 영향을 미칩니다. 이러한 이론들은 많은 종류의 증명, 구조, 추상 대수학에서 사용됩니다. 다른 집합과 공역(codomain)에서 관계를 만드는 것도 집합의 중요한 응용입니다.
컴퓨터 과학에서, 집합 이론은 데이터를 수집해야 하고 그들의 다중성이나 순서에 신경 쓰지 않을 때 유용합니다. 이 페이지에서 보았듯이, 해시 테이블과 집합은 매우 관련이 있습니다. 데이터베이스, 특히 관계형 데이터베이스에서 집합은 매우 유용합니다. 다른 테이블과 데이터 집합의 합집합, 교집합, 차집합을 찾는 많은 명령어가 있습니다.
Minimal Required Functionalities
집합에는 네 가지 기본 연산이 있습니다.
| 함수 이름 | 제공 기능 |
|---|---|
insert(i) |
집합에 i를 추가합니다. |
remove(i) |
집합에서 i를 제거합니다. |
size() |
집합의 크기를 반환합니다. |
contains(i) |
집합이 i를 포함하는지 여부를 반환합니다. |
때로는 두 집합 간의 상호 작용을 허용하는 연산이 구현됩니다.
| 함수 이름 | 제공 기능 |
|---|---|
union(S, T) |
집합 S와 집합 T의 합집합을 반환합니다. |
intersection(S, T) |
집합 S와 집합 T의 교집합을 반환합니다. |
difference(S, T) |
집합 S와 집합 T의 차집합을 반환합니다. |
subset(S, T) |
집합 S가 집합 T의 부분집합인지 여부를 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Time Complexity
모든 추상 자료형과 마찬가지로, 집합을 구현하는 방법은 여러 가지가 있습니다. 해시 테이블이 가장 일반적인 자료 구조이므로, 아래에서 그 시간 복잡도를 살펴보겠습니다.
해시 테이블 삽입 - $O(1)$, 해시 테이블 제거 - $O(1)$, 해시 테이블 포함 여부 확인 - $O(1)$
연관 배열과 달리, 이 해시 테이블 구현에서는 충돌을 어떻게 처리할지 걱정할 필요가 없습니다. 왜냐하면 우리는 충돌을 전혀 처리하지 않기 때문입니다! 충돌이 발생하면, 그 값이 이미 거기에 있다는 것을 의미하며 우리는 아무것도 할 필요가 없습니다! 이것이 해시 테이블을 이용한 집합 구현이 프로그래머들에게 일반적으로 선택되는 이유입니다.
Red-Black Tree
레드-블랙 트리는 이진 탐색 트리의 한 종류입니다. AVL 트리처럼 자가 균형을 맞추지만, 균형 잡힌 상태를 유지하기 위해 다른 속성을 사용합니다. 균형 잡힌 이진 탐색 트리는 불균형 이진 탐색 트리보다 검색 효율이 훨씬 높기 때문에, 균형을 유지하는 데 필요한 복잡성은 종종 그럴 가치가 있습니다. 트리의 각 노드가 빨간색 또는 검은색으로 표시되기 때문에 레드-블랙 트리라고 불립니다.
레드-블랙 트리는 AVL 트리보다 약간 더 느슨한 높이 불변 조건을 유지합니다. 레드-블랙 트리의 높이가 약간 더 크기 때문에, 레드-블랙 트리에서의 조회가 더 느릴 것입니다. 그러나 더 느슨한 높이 불변 조건은 삽입과 삭제를 더 빠르게 만듭니다. 또한, 레드-블랙 트리는 구현의 상대적인 용이성 때문에 인기가 있습니다.
이 이미지는 레드-블랙 트리의 표현을 보여줍니다. 각 리프(leaf)가 실제로는 검은색의 null 값이라는 점에 유의하십시오. 이러한 속성들은 트리의 높이 불변 조건을 증명하는 데 중요할 것입니다.
Red-Black Tree
Overview
레드-블랙 트리는 노드로 구성되어 있고 각 노드가 최대 두 개의 자식을 갖는다는 점에서 이진 탐색 트리와 유사합니다. 그러나 레드-블랙 트리에 특정한 새로운 속성들이 있습니다.
- 각 노드는 빨간색 또는 검은색이며, 이는 메모리에 단일 비트로 저장될 수 있습니다 (예: '빨간색' = 1, '검은색' = 0).
- 트리의 루트는 항상 검은색입니다.
- 모든 리프는 null이며 검은색입니다.
- 노드가 빨간색이면, 그 부모는 검은색입니다.
- 주어진 노드에서 그 자손 리프 중 하나로 가는 모든 경로에는 동일한 수의 검은색 노드가 포함됩니다. 이것은 때때로 **블랙-뎁스(black-depth) 알려져 있습니다.
- 레드-블랙 트리의 높이는 최대 $2⋅\log₂(n+1)$입니다; 이 속성은 나중에 증명될 것입니다.
트리의 높이 불변 조건을 깨뜨리는 특정 노드가 삽입될 때, 트리는 노드의 현재 색상 체계를 사용하여 재배열됩니다. 트리가 재배열된 후, 색상 속성이 유지되도록 다시 칠해집니다.
Red-Black Tree Height
레드-블랙 트리의 높이를 증명하는 것은 특히 중요합니다. 왜냐하면 레드-블랙 트리의 높이가 점근적 복잡도와 성능을 계산할 수 있게 해주기 때문입니다. 다음은 그 방법 중 하나입니다.
먼저 높이가 h인 레드-블랙 트리를 상상해 봅시다. 이제 모든 빨간색 노드를 그들의 검은색 부모 노드로 합칩니다. 주어진 검은색 노드는 다음 중 하나를 가질 수 있습니다.
- 2개의 검은색 자식, 이 경우 검은색 부모는 여전히 2개의 자식을 가집니다.
- 1개의 검은색 자식과 1개의 빨간색 자식, 이 경우 검은색 부모는 이제 3개의 자식을 가집니다.
- 2개의 빨간색 자식, 이 경우 검은색 부모는 이제 4개의 자식을 가집니다.
다음은 그 합병 과정의 그래픽 예시입니다 (벗어난 화살표는 검은색 노드를 가리킨다고 가정).
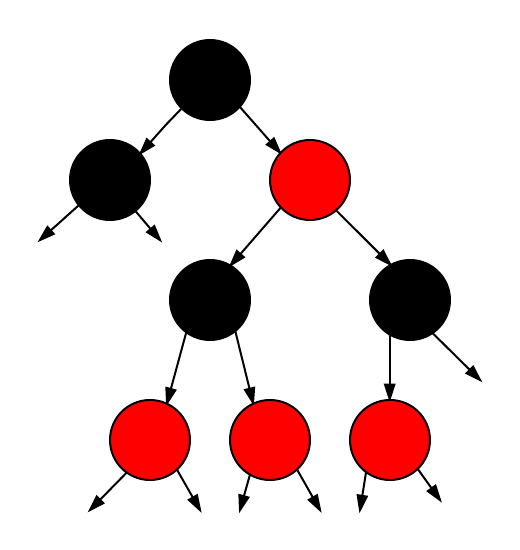 Tree before the merge
Tree before the merge
이제 모든 빨간색 노드를 그들의 부모 노드로 합칩니다. 이는 어떤 검은색 노드든 이제 $2⋅r+2$개의 포인터가 나오게 된다는 것을 의미하며, 여기서 $r$은 그들이 가진 빨간색 자식의 수입니다.
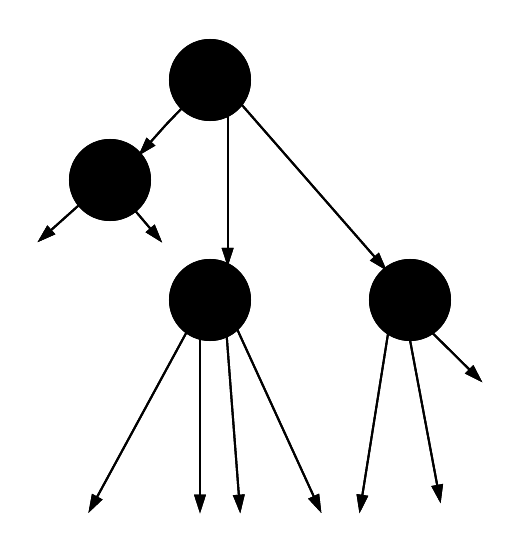 Tree after the merge
Tree after the merge
보시다시피, 모든 검은색 노드는 2, 3, 또는 4개의 자식을 가집니다.
이 새로운 트리는 높이 $h_1$을 가집니다. 원래 레드-블랙 트리에서 어떤 경로든 최대 절반의 노드가 빨간색이었기 때문에, 이 새로운 높이가 원래 높이의 최소 절반이라는 것을 압니다. 그래서,
$h₁ \geq h/2$
트리의 리프 수는 정확히 $n+1$이므로,
$n+1≥2^h₁$ $log₂(n+1)≥h₁≥h/2$ $h≤2log₂(n+1)$.
Operations
레드-블랙 트리에서는 트리의 구조를 변경할 수 있는 두 가지 연산, 즉 삽입과 삭제가 있습니다. 이러한 변경에는 노드의 추가 또는 제거, 노드 색상 변경, 또는 회전을 통한 노드 재구성이 포함될 수 있습니다. 삽입 과정에 대한 다양한 경우와 알고리즘을 보여줌으로써, 우리는 삭제에 대해서도 같은 것을 추론할 수 있습니다.
노드를 삽입하는 것은 먼저 트리를 검색하여 올바른 위치를 찾는 것을 포함합니다. 그런 다음 노드는 빨간색 노드로 삽입됩니다. 이것은 빨간색 노드의 부모가 검은색이라는 속성을 위반할 수 있습니다. 그래서 이제 우리가 처리해야 할 세 가지 잠재적인 경우가 있습니다.
1) 경우 1
첫 번째 경우, 우리가 삽입한 노드는 빨간색, 그 부모도 빨간색, 그리고 부모의 형제도 빨간색입니다. 삽입된 노드의 조부모는 검은색일 것이므로, 우리는 삽입된 노드의 조부모의 색상을 삽입된 노드의 부모와 그 부모의 형제의 색상으로 바꾸기만 하면 됩니다. 이 경우는 삽입된 노드의 조부모가 빨간색 부모를 가질 수 있기 때문에 트리의 루트까지 계속해서 수정해야 할 수도 있습니다.
다음 그래픽은 이 경우를 보여줍니다. 삽입된 노드는 "INSERT"로 표시되어 있습니다. 왼쪽 트리는 경우를 보여주고, 오른쪽 트리는 수정된 것을 보여줍니다.
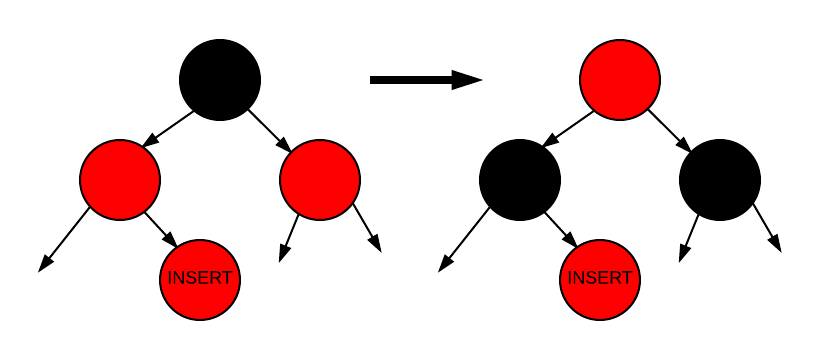 Insertion - Case 1
Insertion - Case 1
2) Case 2
경우 2는 노드의 부모는 빨간색이지만 부모의 형제는 검은색이고, 노드의 값이 부모와 조부모의 값 사이에 있을 때 발생합니다.
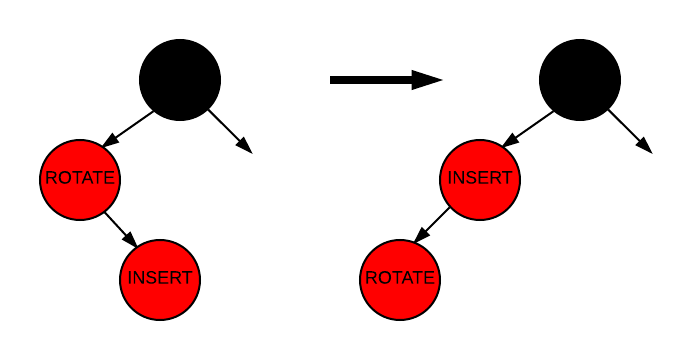
우리는 경우 3으로 이어지는 회전을 수행하여 경우 2를 처리합니다. 왼쪽 회전과 오른쪽 회전 두 종류의 회전이 있습니다. 경우 2는 관련된 노드들이 시계 반대 방향으로 회전하기 때문에 왼쪽 회전을 사용합니다. 다음 이미지는 경우 2에서의 회전을 보여줍니다. 기억하십시오, 이 회전은 문제를 완전히 해결하지는 않지만, 경우 3에서 해결될 수 있도록 준비합니다.
 Insertion - Case 2
Insertion - Case 2
보시다시피, "ROTATE"로 표시된 노드에서 왼쪽 회전이 수행되었습니다.
3) 경우 3
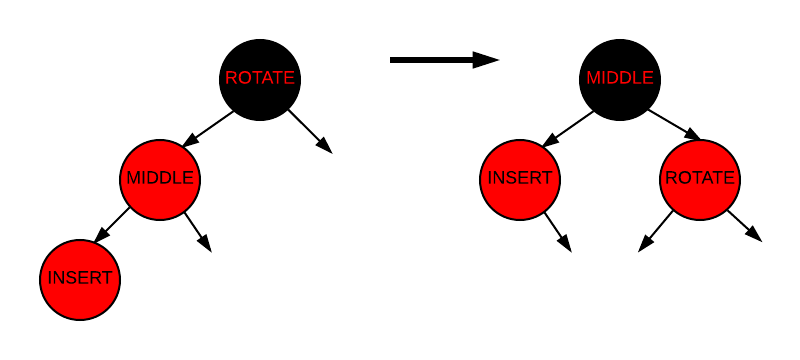
경우 3은 조부모에 대한 오른쪽 회전을 포함합니다. 다음 그래픽에서, 회전할 노드는 "ROTATE"로, 삽입된 노드는 "INSERT"로, 그리고 세 번째 노드 "MIDDLE"은 회전 후 어디로 가는지 보여주기 위해 표시되었습니다.
 Insertion - Case 3
Insertion - Case 3
삭제는 위에서 언급했듯이 정확히 같은 방식으로 작동합니다. 노드가 트리에서 제거되면, 트리는 위의 3가지 경우 중 하나에 해당할 수 있습니다. 그런 다음 문제는 같은 방식으로 해결됩니다.
Asymptotic Complexity
삽입이나 삭제 시에 무엇을 해야 하는지 알았습니다. 그렇다면 각 연산의 실행 시간은 얼마일까요?
앞서 증명했듯이, 높이는 최대 $h≤2⋅\log₂(n+1)$입니다. 이는 삽입하거나 삭제할 수 있는 인덱스를 찾는 과정이 $O(\log₂(n))$ 연산이 될 것임을 의미합니다. 그 시점에서 우리는 세 가지 경우 중 하나에 해당할 수 있습니다.
경우 1에서는 트리를 거슬러 올라가면서 노드를 다시 칠해야 합니다. 이 과정 또한 $O(\log₂(n))$이 걸리므로, 복잡도를 전혀 증가시키지 않습니다.
경우 2와 3에서는 각각 1번 또는 2번의 회전을 수행합니다. 그 시점에서 우리는 종료합니다. 이러한 경우는 상수 시간 연산입니다. 따라서 삽입과 삭제는 $O(\log₂(n))$ 시간이 걸린다는 것을 알 수 있습니다.
레드-블랙 트리에서의 검색은 다른 균형 잡힌 이진 탐색 트리와 마찬가지로 $O(\log₂(n))$ 시간입니다. 순회는 전체 트리를 검색하기 위해 각 노드에 들어가고 나오기만 하면 되므로 $O(n)$의 분할 상환 연산입니다.
| 평균 | |
|---|---|
| 공간 | $O(n)$ |
| 검색 | $O(\log₂(n))$ |
| 순회 | *$O(n)$ |
| 삽입 | $O(\log₂(n))$ |
| 삭제 | $O(\log₂(n))$ |
| *분할 상환 분석 |
Priority Queues
우선순위 큐는 큐를 일반화하는 추상 자료형의 한 종류입니다. 그 원리는 큐에 있는 모든 값에 대해 우선순위를 포함한다는 점을 제외하고는 정확히 동일합니다. 값이 삽입될 때 우선순위가 할당됩니다. 가장 높은 우선순위를 가진 값이 항상 먼저 제거됩니다.
우선순위 큐를 병원처럼 생각할 수 있습니다. 환자를 선입선출(FIFO) 방식으로 치료하는 것은 항상 좋은 생각이 아닙니다. 왜냐하면 일부 환자는 위급한 상태일 수 있기 때문입니다. 그래서 기침을 하는 환자가 와서 낮은 우선순위를 배정받을 수 있습니다. 그런 다음 나중에 총상을 입은 환자가 오면 높은 우선순위를 받고 먼저 치료받게 됩니다.
우선순위 큐는 여러 프로그램과 그 실행을 관리하는 시스템(노트북과 같은)에 매우 중요합니다. 또한 중요한 데이터가 더 빨리 통과하도록 우선순위를 정할 수 있기 때문에 인터넷과 같은 네트워킹 시스템에도 매우 중요합니다.
Minimal Required Functionality
우선순위 큐에는 세 가지 기본 연산이 있습니다.
| 함수 이름* | 제공 기능 |
|---|---|
insert(i, p) |
우선순위 p를 가진 값 i를 추가합니다. |
pop() |
가장 높은 우선순위를 가진 요소를 제거하고 반환합니다. |
peek() |
큐를 변경하지 않고 가장 높은 우선순위를 가진 요소를 반환합니다. |
| *정확한 이름이 요구되는 것은 아닙니다. 실제로 일부 기능은 특정 언어에서 특별한 문법을 통해 직접 제공될 수 있습니다. |
Time Complexity
우선순위 큐는 거의 항상 어떤 종류의 힙을 사용하여 구현됩니다. 따라서 힙을 사용한 우선순위 큐의 시간 복잡도가 가장 일반적으로 보입니다.
힙 삽입 - $O(\log n)$, 힙 추출 - $O(\log n)$, 힙 피크 - $O(1)$
삽입의 경우, 전체 자료 구조를 다시 힙으로 만들어야 할 수도 있습니다. 따라서 삽입 과정 자체는 $O(1)$ 시간이 걸리지만, 힙으로 만드는 과정(heapify)은 $O(\log n)$이 걸립니다. 추출(pop)도 마찬가지입니다. 최대 우선순위 값이 어디에 있는지 알지만, 힙을 다시 만드는 데는 여전히 $O(\log n)$ 시간이 걸립니다. 피크(peek)는 다른 추상 자료형과 마찬가지로 상수 시간 연산입니다.
Applications
우선순위 큐는 너무나 많은 다양한 분야에서 사용되므로, 여기에 모두 나열하는 것은 비현실적입니다. 그들이 도입하는 오버헤드(우선순위)는 보통 그 이점에 비해 미미합니다. 다음은 우선순위 큐가 실제로 사용되는 몇 가지 예입니다.
-
운영 체제 컴퓨터의 운영 체제는 어떤 프로그램이 언제 실행될지를 관리합니다. 프로그램 큐가 가득 찼다고 상상해 보세요. 갑자기, 매우 중요한 새로운 프로그램이 실행되어야 합니다. 운영 체제는 그것을 높은 우선순위로 큐에 넣을 것입니다.
-
그래프 탐색 알고리즘 A* 탐색 및 다익스트라 알고리즘과 같은 많은 효율적인 그래프 탐색 알고리즘은 다음에 탐색할 노드를 알기 위해 우선순위 큐를 사용합니다. 이 응용 프로그램은 네트워킹과 같은 그래프 탐색의 파생 응용도 포함합니다.
-
시간 기반 이벤트 프로그램이 다양한 시간에 실행되어야 하는 많은 이벤트를 가지고 있다면, 프로그램은 우선순위 큐를 사용할 수 있습니다. 우선순위는 프로그램을 실행할 타임스탬프가 될 것입니다. 그러면 큐는 올바르게 정렬될 것입니다.
-
대역폭 관리 큐는 인터넷 및 기타 네트워크에서 데이터 흐름을 처리하는 데 사용됩니다. 그러나 모든 데이터가 똑같이 중요한 것은 아닙니다. 중요한 데이터의 우선순위를 정함으로써, 네트워크는 그것이 가능한 한 빨리 목적지에 도달하도록 보장할 수 있습니다. 우선순위 큐는 종종 이러한 이유로 사용됩니다.
Heaps
힙은 힙 속성에 의해 제약을 받는 트리 기반의 자료 구조입니다. 힙은 최단 경로를 찾는 다익스트라 알고리즘, 힙 정렬, 우선순위 큐 구현 등 많은 유명한 알고리즘에서 사용됩니다. 본질적으로, 힙은 최대 또는 최소 요소에 매우 빠르게 접근하고 싶을 때 사용하고자 하는 자료 구조입니다.
힙에는 여러 변형이 있으며, 각각 장점과 절충점을 제공합니다.
 Example of a complete binary max-heap with node keys being integers from 1 to 100
Example of a complete binary max-heap with node keys being integers from 1 to 100
General Structure
힙은 보통 배열로 구현되며 트리로 생각할 수 있는 자료 구조입니다(포인터를 사용하여 구현될 수도 있습니다). 예를 들어, 아래 이미지에서 배열의 요소들이 어떻게 트리에 매핑되어 최대-힙(부모 노드가 자식 노드보다 큰 값을 갖는 힙)을 만드는지 주목하십시오.
트리 측면에서, 힙의 루트는 가장 위에 있는 요소입니다. 아래 이미지에서 루트는 16입니다. 트리에서 주어진 노드의 높이는 그 노드로부터 리프까지의 가장 긴 경로로 정의되며, 여기서 리프는 트리 맨 아래에 있는 노드입니다.
 Example of a Max Heap (note: 1 indexing)
Example of a Max Heap (note: 1 indexing)
힙 속성에는 최소-힙 속성과 최대-힙 속성 두 가지 일반적인 버전이 있습니다.
최대-힙 속성
만약 A가 힙의 배열 표현이라면, 최대-힙에서:
$A[parent(i)] \geq A[i]$,
이는 노드가 그 부모보다 큰 값을 가질 수 없음을 의미합니다. 최대-힙에서는 가장 큰 요소가 루트에 저장되고, 최소 요소들은 리프에 있습니다.
최소-힙 속성
유사하게, 만약 A가 힙의 배열 표현이라면, 최소-힙에서:
$A[parent(i)] \leq A[i]$,
이는 부모 노드가 그 자식보다 큰 값을 가질 수 없음을 의미합니다. 따라서 최소 요소는 루트에 위치하고, 최대 요소들은 리프에 위치합니다.
사용되는 힙의 종류에 따라, 힙 속성에는 추가적인 요구 사항이 있을 수 있습니다.
최대-힙 속성(또는 최소-힙 속성)을 유지하기 위해, 힙 정렬은 max_heapify(A,i)라는 절차를 사용합니다. 이 함수는 배열 A와 배열의 인덱스 i를 입력으로 받습니다. 이는 min-heapify 함수로 쉽게 변형될 수 있습니다.
본질적으로, 만약 요소 A[i]가 최대-힙 속성을 위반하면, max_heapify는 해당 요소를 트리 아래로 내려보내서 인덱스 i를 루트로 하는 서브트리가 최대 힙이 될 때까지(따라서 위반이 수정될 때까지) 이를 수정합니다.
Minimum Functionalities of Heaps
모든 힙이 구현해야 하는 여러 연산이 있습니다. 사용되는 특정 종류의 힙에 따라, 이러한 연산이 구현되는 방식이 다를 수 있습니다. 특정 힙 구현에서 어떤 연산이 수행되든, 연산이 완료될 때 해당 구현과 관련된 힙 속성이 만족되어야 합니다. 예를 들어, 이진 힙으로 구현된 최소-힙에서 연산을 수행하여 최소-힙 속성을 위반하는 경우, 연산이 완료되기 전에 위반 사항을 수정해야 합니다. 다음은 몇 가지 기본적인 힙 연산입니다.
힙 구성(Build Heap): 힙을 구성할 수 있는 것이 중요합니다.
Build-Heap은 보통Insert와Heapify함수를 반복적으로 사용하여 구현됩니다. 그래서 빈 힙에서 시작하여Insert로 노드를 추가한 다음, 각 단계에서 힙이 힙 속성을 유지하도록Heapify를 호출합니다.힙 속성 유지(Heapify): 힙 속성(위 섹션에서 설명)을 유지하는 데 사용됩니다.
삽입(Insert): 힙에 요소를 추가할 수 있는 것이 중요합니다.
제거(Remove): 힙에서 요소를 삭제할 수 있는 것이 중요합니다.
최소/최대 찾기 및 최소/최대 추출: 힙의 목적에 따라 가장 크거나 작은 요소가 종종 관심의 대상이므로 이러한 연산은 유용합니다.
키 감소/증가: 특정 노드의 키를 변경하는 데 사용됩니다. 키는 힙에서 노드가 위치할 자리를 결정합니다. 따라서 키를 조정하면 알고리즘이 힙의 일부를 재정렬할 수 있습니다.
병합(Merge): 때로는 meld라고도 불리는 병합 함수는 힙을 결합하는 데 유용한 연산입니다.
Types of Heaps
여러 다른 종류의 힙이 있으며, 각각 다른 구현과 다양한 장단점을 가집니다. 그러나 각 힙 유형은 힙 속성을 만족하며 동일한 종류의 작업에 사용될 수 있습니다.
| 힙의 종류 | 삽입 | 삭제 | 키 감소 | 병합 | 최소 추출 |
|---|---|---|---|---|---|
| 이진 힙 | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ | $O(n)$ | $Θ(\log n)$ |
| 피보나치 힙* | $O(1)$ | $O(\log n)$ | $O(1)$ | $O(1)$ | $O(\log n)$ |
| 이항 힙 | $O(1)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ |
| 페어링 힙* | $O(1)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ | $O(\log n)$ |
*분할 상환 실행 시간
Applications
큐
힙은 우선순위 큐를 구현하는 데 사용될 수 있으며, 여기서 먼저 들어온 객체가 큐에서 먼저 나옵니다.
힙 정렬
힙은 힙 정렬 알고리즘에서 사용됩니다. 힙 정렬은 빠르고 공간 효율적인 정렬 알고리즘입니다. 힙 속성을 유지하고 최소 힙과 최대 힙의 정렬된 특성을 활용하여 작동합니다.
다음은 힙 정렬을 보여주는 애니메이션입니다. 리스트로부터 힙이 어떻게 구성되고 최대-힙 속성이 어떻게 적용되는지 주목하십시오.

[!links]